클래스가 주어진 디퓨전 즉, Classifier Guidance Diffusion은 DDPM과 DDIM에 class 정보가 추가로 주어졌을 때의 분포를 학습하는 것이다.
클래스가 주어진 DDPM의 새로운 분포 q_hat에 대한 아래 4가지 기본 정의와 성질을 알아야한다.

4개의 수식에 대해 알아보면, class가 주어지든 주어지지 않든 DDPM의 x0에서의 분포는 동일하며, x0가 주어졌을 때 class의 분포는 완벽히 정의되어있고, y가 주어졌을 때의 forward pass는 DDPM과 동일하고, class가 주어져도 markovian chain rule을 따른다는 것을 확인할 수 있다.
classifier guidance DDPM의 경우 동일하게 denoising 과정, 즉 backward pass에 대한 수식을 정리해야하는데, 아래와 같이 나타낼 수 있다. y가 주어진 backward분포는 bayesian rule에 의해서 우변처럼 나타낼 수 있게 된다.

첫번째로 classifier부분을 먼저 살펴보면, bayesian rule로 정리하고 앞서 정의한 def 3을 활용하고 normalize term으로 정리하면 backward를 진행할 때, 더 최신의(더 x0)와 가까운 지점의 input이 주어졌을 때의 class분포와 동일하다는 것을 알 수 있었다.

두번째로 classifier DDPM 부분을 살펴보면,

위와 같이 정리되고, 파란색 부분을 또 따로 정리하면,

결과적으로, classifier가 있건 없건 동일하게 forward pass 분포를 갖는다는 것을 확인했다.
갈색 부분에 대한 분포를 정리하면,

우선 1:t까지의 과정을 나타내는 분포와 y의 joint 분포를 y에 대해서 적분한 것으로 변형하고, bayesian rule을 적용하고, def 4를 활용하여 정리하고 def 3으로 Original DDPM과 동일함을 나타내면 x0가 주어졌을 떄, 1:t까지의 과정의 분포는 classifier 유무에 관계없이 동일함을 알 수 있다.
그리고 t시점에서의 x의 분포는 classifier가 있는 분포를 우측 식과 같이 t까지의 과정의 분포를 적분하는 식으로 변형할 수 있고 이를 조건부확률로 조정한 후 앞서 증명한 분포로 변형하고 def1도 활용하면 t시점에서의 x의 분포 역시 classifier 유무에 관계없이 동일함을 알 수 있다.
결론적으로 original DDPM의 backward 분포와 backward된 time step에서의 class 분포의 곱으로 표현할 수 있게 된다.

이 분포를 학습하기 위해 아래와 같이 theta와 phi의 파라미터를 사용하여 분포를 표현한다.

결국 이 분포도 가우시안이기 때문에 아래와 같이 평균과 분산으로 표현할 수 있게되고, log를 취하면 다음 이차식과 상수만 남게된다.

그리고 log(y|x_t)의 경우는 Taylor expansion을 활용하여 xt가 mu일때의 값과 xt가 mu일 때 미분한 gradient와 xt-mu를 곱한 식으로 확장을 할 수 있다.
그 식을 정리하면 (6)과 같아지고 g는 xt가 mu일 때의 log(y|x_t)의 gradient를 의미한다.

이렇게 얻어진 log p(xt|x_t+1)과 logp(y|xt)는 (10)번 수식의 평균과 분산처럼 가우시안 분포로 표현할 수 있게 된다.
위 과정은 stochastic diffusion sampling process 즉, DDPM에서는 사용가능하지만 deterministic한 DDIM에서는 사용하기가 어렵다. DDIM에서 생성하고 싶은 것은 xt 뿐만 아니라 class까지 함께 생성하는 것이다. 즉 , joint distribution으로 s(xt,y)를 구하는 것인데, s는 score function으로 아래와 같이 정의된다.
DDIM에서도 쓰기 위해서 score matching과 DDPM을 접목한 score-based conditioning trick 를 사용하기로 했다고 한다. 아래 식이 score function s(t)이자 epsilon(xt)라고 함.
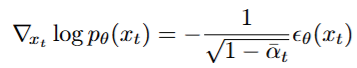
즉, s(xt,y)를 나타내면 아래와 같다.

위 수식은 unconditional일 때의 Classifier Guidance Diffusion모델의 노이즈 분포를 설명한다.
즉, 모든 이미지를 이용하여 생성하되 class 조건을 부여한 것이다. 이 때는 scaling factor를 크게 주어야한다.
그렇다면 conditional일 때의 Classifier Guidance Diffusion모델은 어떨까?
아래 수식을 살펴보면 y라는 조건부가 빨간 글씨로 추가된 것을 확인할 수 있고, 결론적인 수식을 살펴보면 classifier guidance에서는 unconditional과 conditional이 유사한 결과를 보여준다.

conditional이라는 것은 웰시코기 이미지들만 모아서 생성하고 class 조건을 부여하는 것이다. 이때는 scaling factor를 작게 주어도 된다. 두 경우의 결과가 비슷함을 알 수 있다.
=>classifier guidance가 unconditional이면 s를 강하게 conditional이면 약하게 주어도 된다!
아래 그림을 보면 알 수 있듯이 guidance를 적게 주면 이미지들은 다양하게 생성되는 것을 알 수 있다. 하지만 알 수 없는 이미지들이 많이 생성된다. 하지만 guidance를 많이 주면 이미지들의 다양성은 떨어지지만 개라는 이미지들은 많이 생성되는 것을 알 수 있다.

classifier guidance diffusion의 단점은 gradient를 알아야하며, classifier가 있어야 한다는 것이다.
=> 이를 보완하기 위해서 Classifier free Diffusion Guidance라는 후속 논문이 나왔고, 추후에 리뷰할 것이다.