Diffusion은 original data에 gaussian noise를 점진적으로 주입하여 original data를 파괴하는 과정을 의미한다.
DDPM은 forward process에서 데이터에 점진적으로 노이즈를 추가하는 고정된 markov chain을 사용하고, reverse process에서 이를 학습 가능한 Gaussian transitions으로 denoising하는 latent variable model
DDPM 은 데이터 x0를 생성하기 위해 일련의 latent variable x1,x2,…,xT를 사용하는 모델로 각 잠재 변수 xt는 데이터 x0와 동일한 차원을 가진다.

2. Background
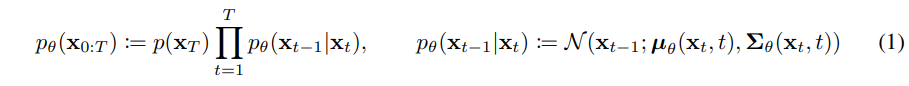
이 모델의 목적은 주어진 데이터 분포에서 새로운 데이터를 생성하는 것으로 reverse process를 나타내는 는 x0부터 xT까지의 전체 latent variable의 결합 분포를 나타내고 p(xT)는 Figure 2의 가장 왼쪽 그림으로 N(xT;0,I) 표준정규분포를 따른다.
여기서 각각의 pθ(xt−1∣xt)는 평균 μθ(xt,t)과 공분산 Σθ(xt,t)를 가지는 Gaussian 분포로 정의되며 (1)식의 우측 식으로 나타낼 수 있다.

forward process를 나타내는 q(x1:T∣x0)는 data에 점진적으로 noise를 추가하는 과정을 의미하고 variance schedule 에 따라 결정되며 (2)의 우측분포로 나타낼 수 있다. 그리고 β는 reparameterization을 통해 학습되거나 하이퍼파라미터로 고정될 수 있다. β변수는 αt:=1−βt로도 표현할 수 있고 그 식은 아래와 같다.


BAYESIAN RULE과 원본이미지를 추가적으로 알았을 조건을 추가하여 다음 식을 도출한다.

위 bayesian rule을 통해 알 수 있듯이 original img를 안다면, forward process를 통해 reverse process의 분포를 정확히 알 수 있게 된다.
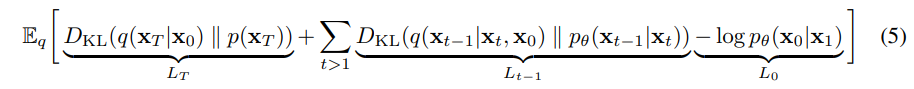

그렇다면 학습을 통해 q(x1:T∣x0)의 분포와 pθ(x0:T)의 분포가 유사하도록 만들어야하는데, L은 (5)로 나타낼 수 있고, 이를 유도하는 과정은 아래와 같다.


다음의 평균값을 줄이는 방향으로 최적화하면 된다. (17) 수식은 아래값으로 변화해서 (18)을 얻을 수 있게 된다.



(18) 식을 t=1일 때와 t>=2일때로 나누어 (19)로 표현하고, q(xt|xt-1)을 위에서 도출한 식을 기반으로 바꾸고 식을 정리하여 (20)을 얻는다.

결과적으로 정리하면 아래와 같은 수식을 얻을 수 있다.




여기서 ut를 구하기 위한 q(xt|xt+1)의 분포는 아래와 같이 구할 수가 있는데

x0를 아래식을 정리해서 대입하게 되면,

아래 식과 같이 x0 를 표현할 수 있게 된다.

그 유도과정은 아래와 같다.




결론적으로 L_{t-1}은 아래 식과 같이 정리되고, epsilon이 변수로 들어가게 된다.


즉, L_T와 L_0는 변수에 영향을 적거나 주지 않으므로 L_t-1만 고려해서 간단히 나타내면 (14)식과 같이 표현할 수 있다.

결론적으로 L을 최적화함으로써 모델을 학습하여 pθ(xt−1∣xt)를 효율적으로 표현할 수 있게된다.
결국 특정 시점에서의 noise를 비교하여 그 차이를 최소화하도록 파라미터를 update하는 것이다. python으로 loss function을 구현한 것은 다음과 같다.
loss function 는 모델이 예측한 노이즈와 실제 추가된 노이즈 사이의 L2 손실(Mean Squared Error, MSE)을 계산하여 모델이 reverse process에서 노이즈를 얼마나 정확히 복원하는지를 평가한다.
# Define variance schedule β_t
beta = torch.linspace(0.0001, 0.02, T) # noise scheduling
alpha = 1.0 - beta
alpha_bar = torch.cumprod(alpha, dim=0)
# Forward diffusion process (q(x_t | x_0))
def forward_diffusion(x0, t):
#x0를 기점으로 t시점까지의 noise 주입
noise = torch.randn_like(x0)
return torch.sqrt(alpha_bar[t]) * x0 + torch.sqrt(1 - alpha_bar[t]) * noise, noise
# Parameter가 포함된 p(x_t-1|x_t)를 나타내는 모델,
# 입력이미지와 차원이 동일하게 출력
model = DenoisingModel()
# Loss function (simple L2 loss between predicted noise and true noise)
def lossfunction(model, x0, t):
xt, true_noise = forward_diffusion(x0, t) # xt는 t시점까지 주입된 노이지 입력, true_noise는 노이즈
xt = xt.view(-1, 28*28) # Flatten for the linear layers
predicted_noise = model(xt, t) # Predict the noise using the model
# L2 loss between the predicted noise and the true noise
loss = F.mse_loss(predicted_noise, true_noise.view(-1, 28*28))
return loss