(논문 수식이해) DDIM method 위주 : DENOISING DIFFUSION IMPLICIT MODELS
DDPM은 forward pass를 markovian chain으로 정의하고, backward pass 역시 gaussian이라는 것을 유도하여 mean과 var를 reparameterization하여 noise를 구하는 방법으로 구하는 방법이였다.
DDPM의 경우는 noise로부터 data로 찾아갈 때 step by step으로 모든 과정을 sampling해야하기 때문에 연산량이 많고 속도가 느리다는 단점이 있었다.
이 문제를 해결하고자 DDIM이 등장한 것이고, 이 DDIM의 기본철학은 DDPM과 Marginal만 동일하게 인공적으로 만들어서 data에서 noise로 denoising되는 전체 과정의 분포는 다르겠지만 각 step마다의 분포는 동일하게 만드는 backward를 정의하는 것이다.
즉, DDIM과 DDPM은 아무 상관없는 다른 분포이지만 marginal은 동일하다. DDIM의 backward에서 variance를 parameter로 부여할 때, step by step을 할 필요없이 건너 뛰어서 data를 생성할 수 있는 것이다.
아래는 DDPM의 분포식 q와 DDIM의 분포식이 q_sigma를 나타낸 것이다.
이때, DDIM의 분포에서 q에 sigma를 붙이는 이유는 sigma는 우리가 마음대로 변화시킬 수 있는 design parameter이기 떄문이다.
* DDPM


* DDIM

이 때 위 수식에서의 alpha value에는 bar가 있어야 함.
DDIM를 정의한 다음분포가 DDPM의 backward 분포와 동일하다는 것을 증명해야지 의미가 생긴다.
증명은 수학적 귀납법을 이용한다. -> DDIM의 marginal분포가 DDPM의 marginal분포와 동일함을 보이면 됨.
1. 수학적 귀납법(Mathematical Induction)
DDIM과 DDPM의 marginal 분포가 동일함을 보임.
i) t= T일때 성립함. -> hold by definition
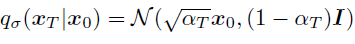

ii) t가 t일때 성립한다고 가정했을 때, t가 t-1도 성립함을 보임.
위 과정을 증명하기 앞서서 marginal and conditional gaussian이면 아래의 수식이 성립함을 알아야한다. 아래 식에서 x가 x_t의 역할을 하고 y가 x_{t-1}이라고 생각하면 증명 과정의 이해가 쉽다.

일단, q_sigma(x_t|x0)는 주어진 상태이고, 그 식은 아래와 같다.
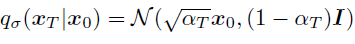
이 때, t-1에서도 성립함을 보이면 되는데, 그 증명과정은 아래와 같다.

우선적으로 모든 분포가 가우시안이라는 것을 확인했고,

gaussian 분포의 특징을 활용해서 x_t-1의 분포를 유도했고, 이는 DDIM은 DDPM과 marginal이 유사하다는 것을 확인했다.
하지만 모두 초기 x0가 주어졌을 때의 분포만을 알기 때문에 p_theta를 KLD를 활용하여 학습해야한다.
2. DENOISING DIFFUSION IMPLICIT MODELS (Objective function 정의)

위 수식은 DDPM의 LOSS FUNCTION이고,

위 수식은 DDIM의 LOSS FUNCTION이다.
DDPM과 DDIM의 비교를 보면, 두 식은 유도된 backward 수식이 학습할 p의 분포와 유사해지도록 KLD를 푼다는 점에서 동일하다. 아래 수식을 보면 알 수 있다.


DDPM은 forward로 정의되어있고, backward를 유도하여 p와의 KL Divergence와 비교해야하기 때문에 오래 걸렸지만, DDIM의 경우 애초에 정의가 backward로 되어 있기 때문에 KL Divergnece를 구할 때, 비교적 간단하다.
식을 유도하면 아래와 같이 3가지 KLD로 나뉘어지고,

2번째 식을 해석하면 DDIM의 fixed 분포를 쫓아서 p의 분포를 학습을 해야한다.
이 때, t가 1일때과 그렇지 않을 때가 다르게 정의되는데,

t>1일 때에 대해서는 q_sigma와 유사해지도록 학습하면 된다.
q_sigma의 분포는 이미 정의되어있고, p의 분포를 학습하기 편리하게 하기 위해 아래와 같이 정의한다.

우리는 backward를 정의했기 때문에 x0를 초기에 알 수 없어서 time step t에서 x0를 유추해야하고 그 것을 f_theta를 활용하여 유추하는 방법을 활용한다. 그래서 위에 f_theta라는 함수가 생긴 것이다.
KLD를 구하는 수식은 아래와 같고, 결국에는 두 분포의 평균의 차이가 가장 중요한 요소이다.

위 식을 활용해서 KLD를 유도해보면, 아래와 같이 정리할 수 있다.

결국 t시점에서 유도되는 x0를 찾아서 일치하도록 학습을 하면되고,
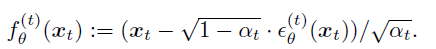

noise로 reparameterization을 하게되면, DDPM과 계수만 다르고 t시점에서의 노이즈를 동일하게 만든다는 점에서는 동일하다.
3. ACCELERATED GENERATION PROCESSES
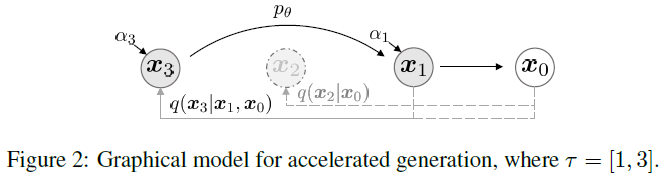
일반적으로 DDPM의 denoising 즉, 생성 과정은 원래 정해진 T단계에 따라 역순으로 진행되므로, 모든 샘플링에 T단계를 거쳐야 한다.
하지만 DDIM의 경우 정의가 backward로 되어있고, marginal만 동일하게 만들었기 때문에 모든 step마다의 경로를 추적할 필요없이 2 step이전 noise이든, 3 step이전 noise이든 분포가 동일할 것이기 때문에 marginal만 같아지고 순서를 건너뛸 수 있도록 정의할 수 있게 되었다.
즉, 전체 T단계 중 몇 개를 골라 S단계로만 forward pass를 정의하고, 그에 대응하는 backward(denoising)을 정의하여 역시 이 S단계만 거치도록 함으로써, 동일한 생성 품질을 유지하면서도 샘플링에 필요한 계산량을 크게 줄일 수 있다.

새롭게 정의된 subset tau에 속한 t와 속하지 않은 t는 다른 network를 정의하여 학습한다.

이 분포 역시 KLD를 활용하여 두 개의 분포가 유사하도록 학습하면 된다. 앞선 2.와 동일하므로 유도과정은 생략하고 수식은 아래와 같다.

결론적으로 DDIM의 특수한 CASE가 DDPM이라고 볼 수 있고, eta=1과 DDPM과 동일한 beta scheduler를 사용하는 경우로, forward가 markov로 정의되는 상황이라는 것을 알 수 있다.
아래에 정의한 eta는 샘플링 과정에서의 분산 설정을 제어하는 파라미터로,
DDIM에서 eta=0으로 설정하면, 샘플링 과정에서 추가적인 가우시안 노이즈를 전혀 넣지 않기 때문에 샘플링 경로가 deterministic해진다.
이 경우에는 이미 정해진 학습된 모델의 분포에 따라 입력 노이즈로부터 고정된 결과를 얻을 수 있으며, 별도의 분산을 학습하거나 추가로 추론할 필요가 없게된다.
eta=1로 두면 DDPM과 동일한 형태의 샘플링을 하게 되며, 이 경우 각 역과정에서 가우시안 노이즈가 주입되므로 샘플링 결과는 확률적이며, 동일한 입력 노이즈라도 결과가 달라질 수 있다.

cf) 여기서 헷갈렸던게 eta가 0이면 deterministic해지면 생성 모델이 아니라는건가?라는 의문이 들었는데, GPT가 나의 궁금증을 해소해주었다.
DDIM 생성 모델로서의 기능을 수행하며, 추가적인 노이즈가 전혀 주입되지 않기 때문에 동일한 초기 조건(예: 같은 x₀)에서 항상 동일한 결과가 생성되는 것이라 출력의 다양성이 감소하지만, 여전히 새로운 이미지를 생성한다.
DDPM : 확률적 샘플링 (eta=1):
동일한 XT에서 시작하더라도, 각 샘플링 과정에서 노이즈가 추가되므로 다양한 X0와 유사한 이미지가 생성.
DDIM : 결정론적 샘플링 (eta=0):
동일한 XT에서 시작하면, 항상 동일한 X0와 유사한 이미지가 생성.
여기서 유사한 이미지는 모델이 학습한 분포에 따라 생성된 새로운 이미지다.
.