(논문 수식이해) VAE method 위주 : Auto-Encoding Variational Bayes
VAE는 쉽게 말하자면,가우시안 분포인 latent z에서 샘플링을하여 decoder를 통과시킨 후 입력 데이터와 유사한 데이터를 생성하는 것을 의미한다.
*AE와 비교해보면 AE는 encoder를 거쳐 입력 이미지의 차원을 축소하여 latent vector로 표현하고 이를 다시 decoder를 거쳐 복원하여 입력 이미지와 동일한 출력 이미지를 얻는 것이다. 이에 반해 VAE는 입력 이미지의 차원을 축소한 latent vector z의 분포도 중요한 정보이고 이 z의 분포의 평균과 표준편차를 구한 후 z 분포에서 랜덤하게 sampling하여 sampling된 latent vector를 decoder에 거쳐 입력과 유사한 다양한 출력 이미지를 얻는 것이다.
본격적으로 논문을 살펴보자.
2.1 Problem scenario
데이터셋이 continuous하거나 discrete한 변수 x로 구성된 dataset X가 있다고 하자. 각각의 data sample은 관찰되지 않은 continuous한 random variable z로 생성되었고, 이 z는 random process를 따른다. prior p(z)를 따르는 z^i와 likelihood p(x|z)를 따르는 x^i로 2 step으로 data를 찾을 수 있다. 하지만 이 p(z)와 p(x|z)의 실제 parameter theta를 구하기 어렵고 z^i 역시 알기 어렵다.
Problem 1. Intractability
marginal likelihood p(x)를 구하기 위해서는 모든 잠재변수 z에 대한 p(z), p(x|z)를 적분해야하는데, 수학적으로 구하기 어렵다. 또한 posterior인 p(z|x)도 복잡한 계산으로 구하기 어렵다는 단점이 있다.
그래서 VB(Variational Bayesian)을 사용하려고 해도, 앞서 말했듯 적분해야할 값이 너무 많아 구하기 어렵다.
Problem 2. Large dataset
데이터가 너무 많아서 모든 데이터를 한 번에 처리하는 batch optimization는 계산 비용이 너무 큽니다. 대신 작은 minibatch나 개별 데이터 포인트를 사용해 모델을 업데이트해야 합니다.
Solution 1. Efficient approximate ML or MAP estimation for the parameters θ.
모델 파라미터 θ 를 효율적으로 추정하는 방법이 필요. (VAE)
Solution 2. Efficient approximate posterior inference of the latent variable z given an observed value x
for a choice of parameters θ.
주어진 x를 기반으로 z를 효율적으로 추정하는 방법이 필요. (Enc)
Solution 3. Efficient approximate marginal inference of the variable x.
z없이 x에 대해 확률적 추론을 할 수 있는 방법이 필요.
* 주어진 데이터 x로부터 잠재 변수 z의 분포를 생성하는 recognition model qϕ(z∣x)과 주어진 잠재 변수 z에서 데이터를 생성하는 모델인 Pθ(x∣z)를 학습하는 과정을 거침.
2.2 The variational bound
본 논문에서는 marginal likelihood를 구하는 것이 목표이다. 하지만 이 값을 직접 계산하는 것이 어렵기 때문에 VBO를 이용하여 근사적으로 계산하는 과정을 거친다.

marginal likelihood는 위 식과 같이 KL Divergence와 Loss term으로 나뉘게 된다. 증명과정은 아래와 같다.

KL Divergence term(주황색)은 실제분포와 추정분포가 유사해지도록 즉 이 값이 작아지도록 하는 것이 최적화하는 방법이다. 하지만 p(z|x)를 모르기 때문에 직접적으로 구할 수 없다. 그 말은 Loss term(파랑색)을 최대화하면 된다는 의미이다.
또 좌변의 log p(x)는 고정된 상수이기 때문에 KL값이 가장 작아도 0이라는 점을 고려하면 log p(x)는 loss term보다 항상 크거나 같다. 이 식은 아래와 같이 표현할 수 있게 된다.

위 식은 Loss term을 q(z|x)를 따르는 log p(x,z) - log q(z|x)의 평균이라고 해석한 것이다.
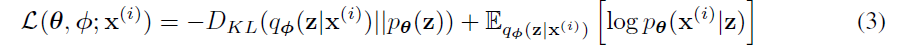
loss term만 따로 정리하면 위와 같고, 그 과정은 아래와 같다.

파란색부분은 reconstruction loss라고 부르며, sampling된 latent variable z에서 x를 reconstruction하는 능력을 평가하는 term으로 이 값이 클수록 재구성을 잘한다는 의미이다.
주황색부분은 KL loss라고 부르며, x로부터 표현된 z의 분포(likelihood)가 사전에 정의된 분포(prior), 예를 들면 가우시안,과 얼마나 유사한지를 나타낸다. 이 값이 작으면 ϕ가 가우시안 분포를 잘 표현한다는 의미이다.
2.3 The SGVB estimator and AEVB algorithm
이 분포를 최적화하기 위해서 주어진 L(θ,ϕ;x)를 파라미터 θ와 ϕ에 대해 미분해야한다.
하지만 파란색 term을 보면 Monte Carlo 추정기에서는 z를 샘플링한 후, 이 샘플들을 이용해 기대값을 추정하는 것을 볼 수 있다. 이를 최적화하기 위해서 logqϕ(z∣x)를 직접 미분하는 방식을 사용하면 불안정하고 분산이 높아서 실용적이지 않고 계산이 복잡하다는 문제가 있다. 이를 다루는 효율적인 방법이 SGVB와 AEVB이다.
1. SGVB 추정기(Stochastic Gradient Variational Bayes Estimator)
z를 분포에서 직접 sampling하는 방법 대신에 reparameterization을 사용하여 z를 계산한다.

sampling과정에 noise variable ϵ으로 변환하여 z를 미분가능한 함수로 변환시킨다.
그렇게 되면, 실제로 ϵ으로부터 샘플링하여 함수 f(z)의 기대값을 추정할 수 있음을 의미한다.

L번 샘플링을 통해 평균을 구함으로써 추정치의 분산을 줄이고 안정적인 학습을 가능하게 한다.
2. AEVB 알고리즘(Auto-Encoding Variational Bayes Algorithm)
AEVB 알고리즘은 SGVB 추정기를 사용해 VAE를 학습하는 방법이다. ELBO를 최대화하기 위해 파라미터 와 ϕ를 업데이트하는 알고리즘으로, Decoder 파라미터 θ와 Encoder 파라미터 ϕ를 최적화하여 데이터의 latent space를 학습하는 과정을 의미한다.


(6)에서 제안한 ELBO term을 더 간단하게 해석할 수 있게 되는데, KL 발산을 직접 계산할 수 있는 상황에서는, 이를 따로 샘플링할 필요가 없이 계산량을 줄일 수 있다고 한다.
즉, KL 발산을 정규화 항목으로 해석하여, 근사된 사후 분포가 사전 분포와 유사하도록 만들게 되는 것이다.
SGVB 추정기의 두 번째 버전은 더 간단한 형태를 가지고 (7)로 z는 전체 데이터셋에서 한번만 계산하면 된다.
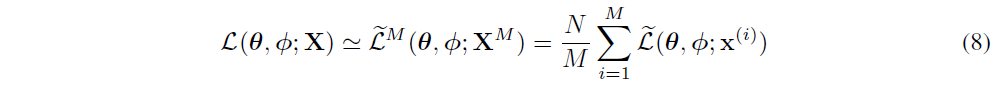
식 (8)은 은 미니배치로 선택된 M개의 데이터들, N은 전체 데이터셋의 크기를 나타내고, 미니배치 최적화를 통해 전체 데이터셋에 대한 ELBO를 구할 수 있게 된다.
2.4 The reparameterization trick
The reparameterization trick 은 복잡한 샘플링 과정에서 파라미터의 gradient를 계산할 수 있으며, 다양한 분포에 적용할 수 있다. 쉽게 이해할 수 있는 예로, 가우시안 분포가 있는데,

z를 직접 샘플링하지 않고도 미분 가능한 형태로 바꿀 수 있게 되는 것이다.
이 밖에도, 지수 분포, 로지스틱 분포, 카우시 분포 등 Inverse CDF를 이용한 방법 / 라플라스 분포, 스튜던트 t 분포, 로지스틱 분포, 가우시안 분포 등 Location-Scale Family / 합성방법 ( 로그-정규 분포는 정규 분포 변수의 지수 변환으로 표현할 수 있고, 감마 분포는 지수 분포 변수들의 합) 등이 있다.
3. VAE
최종적으로, 데이터 에 대해 VAE의 손실 함수는 다음과 같이 계산된다. 손실 함수를 통해 KL 발산을 최소화하면서 재구성 오류를 최소화하는 방식으로 VAE를 학습시킨다.
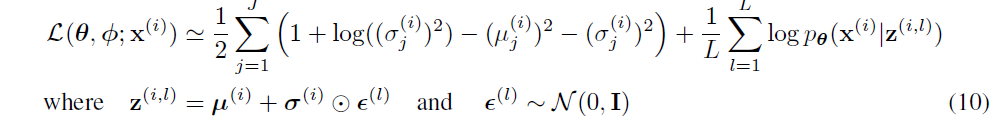
KLD의 유도과정은 아래와 같다.


Reconstruction term의 경우 sampling과정을 reparameterization trick을 사용해서 미분가능하게 만들었다는 증명은 아래와 같다.

최종적으로 model의 개괄적인 코드 구성과 loss function 정의 코드는 아래와 같다.
class VAE(nn.module):
def __init__(self, Encoder, Decoder):
super(VAE, self).__init__()
self.Encoder = Encoder
self.Decoder = Decoder
def reparameterization(self, mean, var):
epsilon = torch.randn_like(var).to(device)
z = mean + var * epsilon
return z
def forward(self, x):
mean, log_var = self.Encoder(x)
z = self.reparameterization(mean, torch.exp(0.5*log_var))
x_hat = self.Decoder(z)
return x_hat, mean, log_vardef loss_funtion(x,x_hat,mean,log_var):
reconstruction_loss = nn.functional.binary_cross_entropy(x_hat,x, reduction='sum')
KLD = -0.5*torch.sum(1 + log_var - mean.pow(2) - log_var.exp())
return reconstruction_loss + KLD